The Benefit's Of Central Limit Theorem

When to use it, How to use it, Where to use it, clearly Understand :)

Altafansari - Medium

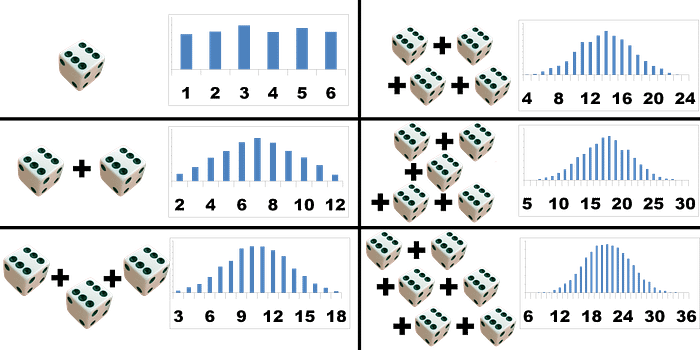
The Central Limit Theorem states that no matter how the distribution of the population is if I take a sufficiently large number of random sample’s (sample1, sample2, sample3, sample4 and so on…) from the population and try to calculate the mean of sample’s and try to plot it then the sampling distribution of the sample mean will be normally distributed.

The two most important concept of the CLT (Central Limit Theorem)

1. Of all the sample’s if we take a average mean then that mean will be the representative of the population mean.
2. The standard deviation of the sample means equals the standard error of the population mean.

Assumption’s behind the CLT

1. The data must follow the randomization condition it must be sampled randomly.
2. Samples should be independent of each other.
3. Sample size should be not more than 10% of the population when sampling is done without replacement.
4. The sample size should be sufficient large.

Use Of Central Limit Theorem

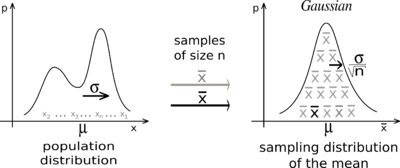
Suppose we have to calculate the average height of the student from 100 different school and in each school the number of students are 2k to 3k so going to each school and calculate the height of each and every individual is difficult so the best idea in this case is to use CLT aka Central Limit Theorem to make the calculation easy because by using CLT we knows that the sample mean will, be near to the population mean as the sample size increases so the sample average height will be equal or near to the population mean height. So if we don’t know the population mean with the help of CLT we can estimate it with the help of sample mean.

Central Limit Theorem Formula

The CLT is applicable for a sufficiently large number of sample size

(n >= 30). The formula for CLT can be stated as follows

Other area’s where CLT is used

A) Election Polls

B) Average Family Income

Conclusion

The advantage of the CLT is that it is powerful, meaning implying that regardless of whether the data originates from an assortment of distributions if their mean and variance are the equivalent, the theorem can even now be utilized.

The CLT notes that the sample means converge on the population means and the distance between them converges to be normally distributed with a variance equal to the population variance as the sample size increases. It is important in the application of statistics and in the understanding of nature.